Why is it useful to be able to find emergent laws? Can we judge how reliable the prediction, that an always-observed pattern will repeat, really is?
Meta Laws for prices of used cars:
Going back to the example about the mean prices of VWs and Renaults, we have seen that the emergent law about more-expensive VWs in T=1750 sequences was verified 185.03 times.
Our idea is trying to find other laws that were verified 185.03 times in the past. If we can find enough of them, we can look how often the prediction, that the pattern will hold, was true.
For this purpose, we constructed an algorithm that searches in databases for laws in all subsamples (chronologically sorted). If one is found (with size of the set of emergence T) at time t, the prediction that the pattern will repeat is evaluated at time t+T. So we can count predictions as well as verifications of patterns and empirically calculate the rate of true predictions. We call this measure “Reliability”.
Rel(DiV) = Number of true Predictions / Total Number of Predictions
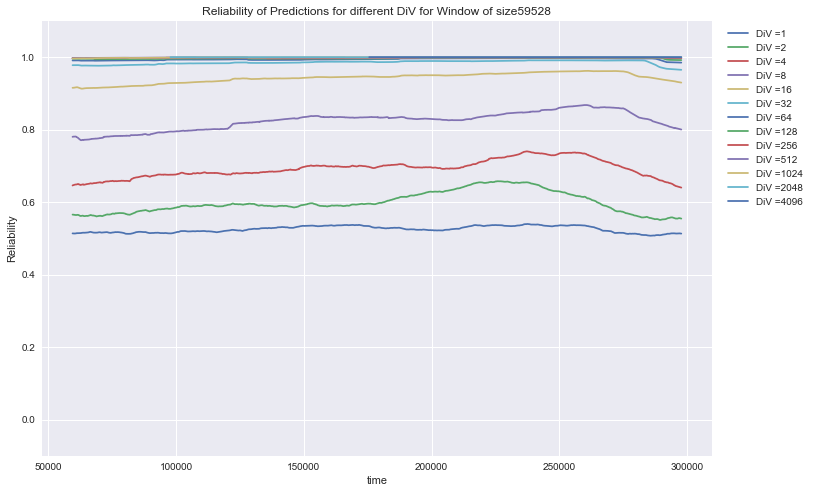
The graph shows the time path of the Reliability for different DiV-classes:
We see that the prediction, that an only once-verified pattern will repeat for a second time was only true for slightly more than 50% of the cases. The reliability of twice verified patterns to was always higher than that. In general, reliability increases with higher DiV and the overall structure is very stable.
Therefore we can find emergent laws about the reliability of predictions for the used-cars-pricing problem as shown in the following table:
| Relation | Div_Laws | Div_MetaLaws | TU_ot |
| Rel > 0.5 | 1 | 8.125458 | 134217728 |
| Rel > 0.5 | 2 | 19.761557 | 16777216 |
| Rel > 0.6 | 4 | 4.823939 | 33554432 |
| Rel > 0.7 | 8 | 9.302647 | 8388608 |
| Rel > 0.9 | 16 | 3.909044 | 8388608 |
| Rel > 0.95 | 32 | 4.712804 | 4194304 |
| Rel > 0.95 | 64 | 6.695429 | 2097152 |
| Rel > 0.99 | 128 | 3.721832 | 2097152 |
| Rel > 0.99 | 256 | 10.843693 | 524288 |
| Rel > 0.99 | 512 | 47.820816 | 65536 |
| Rel > 0.999 | 1024 | 1.935173 | 524288 |
| Rel > 0.999 | 2048 | 14.181244 | 32768 |
| Rel > 0.999 | 4096 | 34.177246 | 2048 |
In the above table we can see for example the following meta-law: For each sequence of TU_ot=524288 predictions with laws of 128<DiVd<=256 the rate of true predictions was at least 99%.
We think that this conclusion is an example for the kind of reasoning that solves the epistemological induction problem:
Using the fact that a pattern was DiV-times verified we can conclude the empirical lower bound of the rate of correct predictions.
Is this a universal, empirical result? Are we also able to find meta-laws for other prediction problems? The following graphs show the time-path of Rel(DiV) for different prediction problems in various domains ranging from natural sciences over business administration and social sciences to sports.
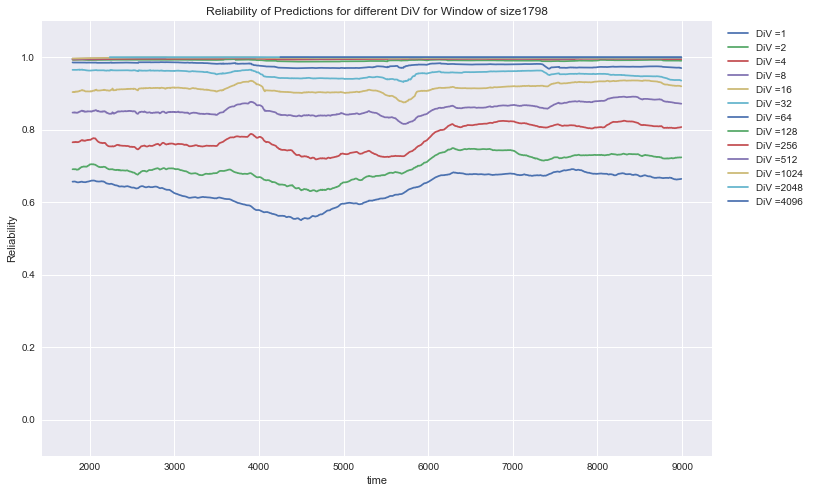
AirQuality: Rel (DiV) for the prediction of 6 different variables of air-pollution
 |
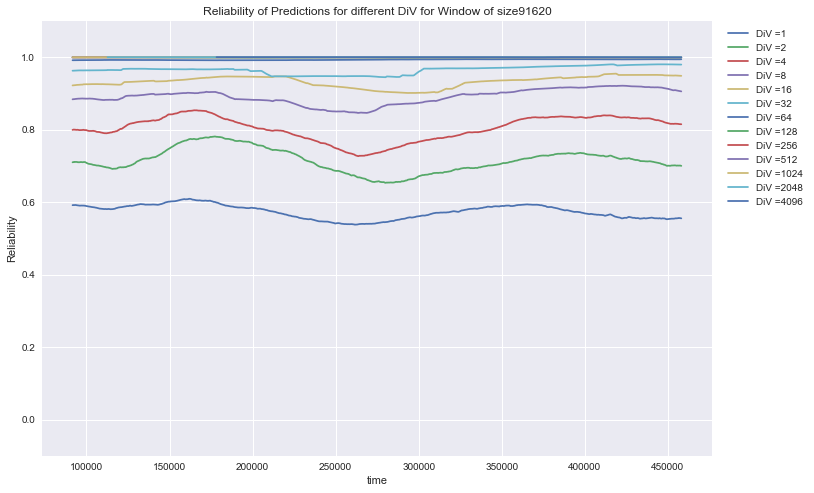
Lending Club: Rel (DiV) for the prediction of 3 different variables of performance of bank loans
 |
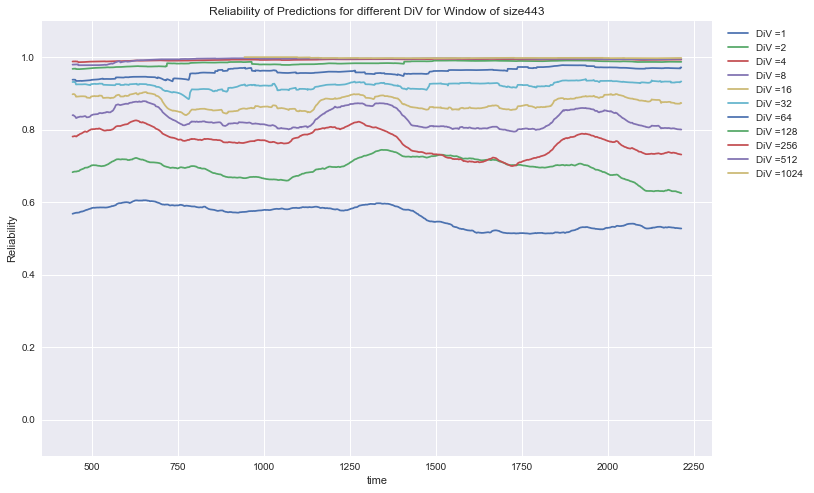
Crime: Rel (DiV) for the prediction of 18 different variables of crime in the US
 |
Soccer: Rel (DiV) for the prediction of 6 different variables of soccer results in Europe
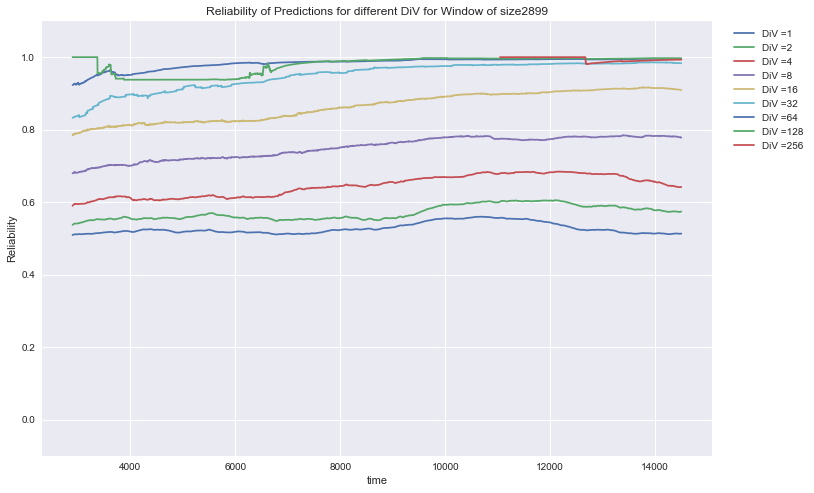 |
The resulting meta-laws for the different domains are not identical but very similar:
| DiV_Laws | AirQuality | Lending Club | Crime | Soccer |
| 1 | Rel > 0.5 | Rel > 0.5 | Rel > 0.5 | Rel > 0.5 |
| 2 | Rel > 0.6 | Rel > 0.6 | Rel > 0.6 | Rel > 0.5 |
| 4 | Rel > 0.7 | Rel > 0.7 | Rel > 0.7 | Rel > 0.6 |
| 8 | Rel > 0.8 | Rel > 0.8 | Rel > 0.8 | Rel > 0.7 |
| 16 | Rel > 0.8 | Rel > 0.9 | Rel > 0.8 | Rel > 0.8 |
| 32 | Rel > 0.9 | Rel > 0.95 | Rel > 0.9 | Rel > 0.95 |
| 64 | Rel > 0.95 | Rel > 0.99 | Rel > 0.9 | Rel > 0.99 |
| 128 | Rel > 0.95 | Rel > 0.99 | Rel > 0.95 | Rel > 0.99 |
| 256 | Rel > 0.99 | Rel > 0.999 | Rel > 0.99 | |
| 512 | Rel > 0.99 | Rel > 0.999 | Rel > 0.99 | |
| 1024 | Rel > 0.99 | Rel > 0.999 | Rel > 0.99 | |
| 2048 | Rel > 0.999 | Rel > 0.999 | ||
| 4096 | Rel > 0.999 | Rel > 0.999 |
Combining the results from all prediction problems analyzed so far, we found universal laws about the empirical lower limits of reliability. We can confidently state that universal emergent laws for lower limits of prediction performance exist across all our analyzed prediction problems in various domains.
Naturally, we do not claim that these laws are a metaphysical, eternal truth – they still can be empirically falsified in the future. But as we gained a lot of experience in using meta-laws instead of probability-based assumptions to guide our model-building processes, we can state that recursive utilization of emergent laws leads to convincing results.